Understanding map and apply
In this series of posts, I'll attempt to describe some of the core functions for dealing with generic data types (such as Option and List).
This is a follow-up post to my talk on functional patterns.
Yes, I know that I promised not to do this kind of thing, but for this post I thought I'd take a different approach from most people. Rather than talking about abstractions such as type classes, I thought it might be useful to focus on the core functions themselves and how they are used in practice.
In other words, a sort of "man page" for map, return, apply, and bind.
So, there is a section for each function, describing their name (and common aliases), common operators, their type signature, and then a detailed description of why they are needed and how they are used, along with some visuals (which I always find helpful).
Haskellers and category-theorists may want to look away now! There will be no mathematics and quite a lot of hand-waving. I am going to avoid jargon and Haskell-specific concepts such as type classes and focus on the big picture as much as possible. The concepts here should be applicable to any kind of functional programming in any language.
I know that some people might dislike this approach. That's fine. There is no shortage of more academic explanations on the web. Start with this and this.
Finally, as with most of the posts on this site, I am writing this up for my own benefit as well, as part of my own learning process. I don't claim to be an expert at all, so if I have made any errors please let me know.
Background
To start with, let me provide the background and some terminology.
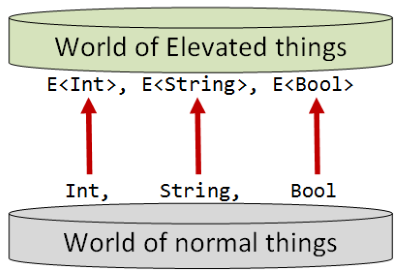
Imagine that there are two worlds that we could program in: a "normal" everyday world and a world that I will call the "elevated world" (for reasons that I will explain shortly).
The elevated world is very similar to the normal world. In fact, every thing in the normal world has a corresponding thing in the elevated world.
So, for example, we have the set of values called Int in the normal world, and in the elevated world there is a parallel set of values called, say, E<Int>.
Similarly, we have the set of values called String in the normal world, and in the elevated world there is a parallel set of values called E<String>.
Also, just as there are functions between Ints and Strings in the normal world, so there are functions between E<Int>s and E<String>s in the elevated world.
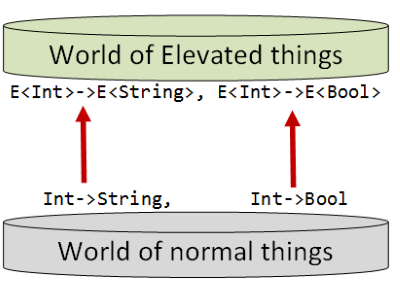
Note that I am deliberately using the term "world" rather than "type" to emphasis that the relationships between values in the world are just as important as the underlying data type.
What exactly is an elevated world?
I can't define what an elevated world is exactly, because there are too many different kinds of elevated worlds, and they don't have anything in common.
Some of them represent data structures (Option<T>), some of them represent workflows (State<T>),
some of them represent signals (Observable<T>), or asychronous values (Async<T>), or other concepts.
But even though the various elevated worlds have nothing in common specifically, there are commonalities in the way they can be worked with. We find that certain issues occur over and over again in different elevated worlds, and we can use standard tools and patterns to deal with these issues.
The rest of this series will attempt to document these tools and patterns.
Series contents
This series is developed as follows:
- First, I'll discuss the tools we have for lifting normal things into the elevated world. This includes functions such as
map,return,applyandbind. - Next, I'll discuss how you can combine elevated values in different ways, based on whether the values are independent or dependent.
- Next, we'll look at some ways of mixing lists with other elevated values.
- Finally, we'll look at two real-world examples that put all these techniques to use, and we'll find ourselves accidentally inventing the Reader monad.
Here's a list of shortcuts to the various functions:
- Part 1: Lifting to the elevated world
- Part 2: How to compose world-crossing functions
- Part 3: Using the core functions in practice
- Part 4: Mixing lists and elevated values
- Part 5: A real-world example that uses all the techniques
- Part 6: Designing your own elevated world
- Part 7: Summary
Part 1: Lifting to the elevated world
The first challenge is: how do we get from the normal world to the elevated world?
First, we will assume that for any particular elevated world:
- Every type in the normal world has a corresponding type in the elevated world.
- Every value in the normal world has a corresponding value in the elevated world.
- Every function in the normal world has a corresponding function in the elevated world.
The concept of moving something from the normal world to the elevated world is called "lifting" (which is why I used the term "elevated world" in the first place).
We'll call these corresponding things "lifted types" and "lifted values" and "lifted functions".
Now because each elevated world is different, there is no common implementation for lifting, but we can give names to the various "lifting" patterns, such as map and return.
NOTE: There is no standard name for these lifted types. I have seen them called "wrapper types" or "augmented types" or "monadic types". I'm not really happy with any of these names, so I invented a new one! Also, I'm trying avoid any assumptions, so I don't want to imply that the lifted types are somehow better or contain extra information. I hope that by using the word "elevated" in this post, I can focus on the lifting process rather than on the types themselves.
As for using the word "monadic", that would be inaccurate, as there is no requirement that these types are part of a monad.
The map function
Common Names: map, fmap, lift, Select
Common Operators: <$> <!>
What it does: Lifts a function into the elevated world
Signature: (a->b) -> E<a> -> E<b>. Alternatively with the parameters reversed: E<a> -> (a->b) -> E<b>
Description
"map" is the generic name for something that takes a function in the normal world and transforms it into a corresponding function in the elevated world.
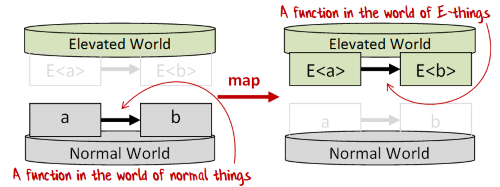
Each elevated world will have its own implementation of map.
Alternative interpretation
An alternative interpretation of map is that it is a two parameter function that takes an elevated value (E<a>) and a normal function (a->b),
and returns a new elevated value (E<b>) generated by applying the function a->b to the internal elements of E<a>.

In languages where functions are curried by default, such as F#, both these interpretation are the same. In other languages, you may need to curry/uncurry to switch between the two uses.
Note that the two parameter version often has the signature E<a> -> (a->b) -> E<b>, with the elevated value first and the normal function second.
From an abstract point of view, there's no difference between them -- the map concept is the same -- but obviously,
the parameter order affects how you might use map functions in practice.
Implementation examples
Here are two examples of how map can be defined for options and lists in F#.
/// map for Options
let mapOption f opt =
match opt with
| None ->
None
| Some x ->
Some (f x)
// has type : ('a -> 'b) -> 'a option -> 'b option
/// map for Lists
let rec mapList f list =
match list with
| [] ->
[]
| head::tail ->
// new head + new tail
(f head) :: (mapList f tail)
// has type : ('a -> 'b) -> 'a list -> 'b list
These functions are built-in of course, so we don't need to define them, I've done it just to show what they might look for some common types.
Usage examples
Here are some examples of how map can be used in F#:
// Define a function in the normal world
let add1 x = x + 1
// has type : int -> int
// A function lifted to the world of Options
let add1IfSomething = Option.map add1
// has type : int option -> int option
// A function lifted to the world of Lists
let add1ToEachElement = List.map add1
// has type : int list -> int list
With these mapped versions in place you can write code like this:
Some 2 |> add1IfSomething // Some 3
[1;2;3] |> add1ToEachElement // [2; 3; 4]
In many cases, we don't bother to create an intermediate function -- partial application is used instead:
Some 2 |> Option.map add1 // Some 3
[1;2;3] |> List.map add1 // [2; 3; 4]
The properties of a correct map implementation
I said earlier that the elevated world is in some ways a mirror of the normal world. Every function in the normal world has a corresponding function in the elevated world,
and so on. We want map to return this corresponding elevated function in a sensible way.
For example, map of add should not (wrongly) return the elevated version of multiply, and map of lowercase should not return the elevated version of uppercase!
But how can we be sure that a particular implementation of map does indeed return the correct corresponding function?
In my post on property based testing I showed how a correct implementation of a function can be defined and tested using general properties rather than specific examples.
This is true for map as well. The implementation will vary with the specific elevated world, but in all cases,
there are certain properties that the implementation should satisfy to avoid strange behavior.
First, if you take the id function in the normal world, and you lift it into the elevated world with map,
the new function must be the same as the id function in the elevated world.
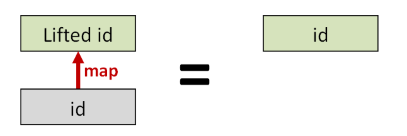
Next, if you take two functions f and g in the normal world, and you compose them (into h, say), and then lift the resulting function using map,
the resulting function should be the same as if you lifted f and g into the elevated world first, and then composed them there afterwards.
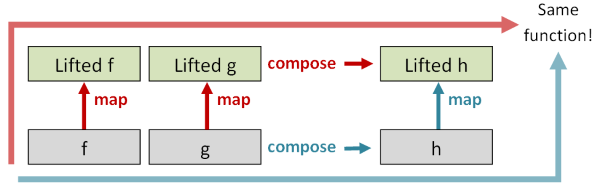
These two properties are the so-called "Functor Laws",
and a Functor (in the programming sense) is defined as a generic data type -- E<T> in our case -- plus a map function that obeys the functor laws.
NOTE: "Functor" is a confusing word. There is "functor" in the category theory sense, and there is "functor" in the programming sense (as defined above).
There are also things called "functors" defined in libraries, such as the Functor type class in Haskell,
and the Functor trait in Scalaz,
not to mention functors in SML and OCaml (and C++),
which are different yet again!
Conseqently, I prefer to talk about "mappable" worlds. In practical programming, you will almost never run into a elevated world that does not support being mapped over somehow.
Variants of map
There are some variants of map that are common:
- Const map. A const or "replace-by" map replaces all values with a constant rather than the output of a function. In some cases, a specialized function like this can allow for a more efficient implementation.
- Maps that work with cross-world functions. The map function
a->blives entirely in the normal world. But what if the function you want to map with does not return something in the normal world, but a value in another, different, enhanced world? We'll see how to address this challenge in a later post.
The return function
Common Names: return, pure, unit, yield, point
Common Operators: None
What it does: Lifts a single value into the elevated world
Signature: a -> E<a>
Description
"return" (also known as "unit" or "pure") simply creates a elevated value from a normal value.
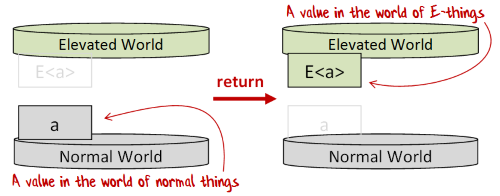
This function goes by many names, but I'm going to be consistent and call it return as that is the common term for it in F#, and is the term used in computation expressions.
NOTE: I'm ignoring the difference between pure and return, because type classes are not the focus of this post.
Implementation examples
Here are two examples of return implementations in F#:
// A value lifted to the world of Options
let returnOption x = Some x
// has type : 'a -> 'a option
// A value lifted to the world of Lists
let returnList x = [x]
// has type : 'a -> 'a list
Obviously, we don't need to define special functions like this for options and lists. Again, I've just done it to show what return might look for some common types.
The apply function
Common Names: apply, ap
Common Operators: <*>
What it does: Unpacks a function wrapped inside a elevated value into a lifted function E<a> -> E<b>
Signature: E<(a->b)> -> E<a> -> E<b>
Description
"apply" unpacks a function wrapped inside a elevated value (E<(a->b)>) into a lifted function E<a> -> E<b>

This might seem unimportant, but is actually very valuable, as it allows you to lift a multi-parameter function in the normal world into a multi-parameter function in the elevated world, as we'll see shortly.
Alternative interpretation
An alternative interpretation of apply is that it is a two parameter function that takes a elevated value (E<a>) and a elevated function (E<(a->b)>),
and returns a new elevated value (E<b>) generated by applying the function a->b to the internal elements of E<a>.
For example, if you have a one-parameter function (E<(a->b)>), you can apply it to a single elevated parameter to get the output as another elevated value.

If you have a two-parameter function (E<(a->b->c)>), you can use apply twice in succession with two elevated parameters to get the elevated output.

You can continue to use this technique to work with as many parameters as you wish.
Implementation examples
Here are some examples of defining apply for two different types in F#:
module Option =
// The apply function for Options
let apply fOpt xOpt =
match fOpt,xOpt with
| Some f, Some x -> Some (f x)
| _ -> None
module List =
// The apply function for lists
// [f;g] apply [x;y] becomes [f x; f y; g x; g y]
let apply (fList: ('a->'b) list) (xList: 'a list) =
[ for f in fList do
for x in xList do
yield f x ]
In this case, rather than have names like applyOption and applyList, I have given the functions the same name but put them in a per-type module.
Note that in the List.apply implementation, each function in the first list is applied to each value in the second list, resulting in a "cross-product" style result.
That is, the list of functions [f; g] applied to the list of values [x; y] becomes the four-element list [f x; f y; g x; g y]. We'll see shortly that this is not the only
way to do it.
Also, of course, I'm cheating by building this implementation on a for..in..do loop -- functionality that already exists!
I did this for clarity in showing how apply works. It's easy enough to create a "from scratch" recursive implementation,
(though it is not so easy to create one that is properly tail-recursive!) but I want to focus on the concepts not on the implementation for now.
Infix version of apply
Using the apply function as it stands can be awkward, so it is common to create an infix version, typically called <*>.
With this in place you can write code like this:
let resultOption =
let (<*>) = Option.apply
(Some add) <*> (Some 2) <*> (Some 3)
// resultOption = Some 5
let resultList =
let (<*>) = List.apply
[add] <*> [1;2] <*> [10;20]
// resultList = [11; 21; 12; 22]
Apply vs. Map
The combination of apply and return is considered "more powerful" than map, because if you have apply and return,
you can construct map from them, but not vice versa.
Here's how it works: to construct a lifted function from a normal function, just use return on the normal function and then apply.
This gives you the same result as if you had simply done map in the first place.
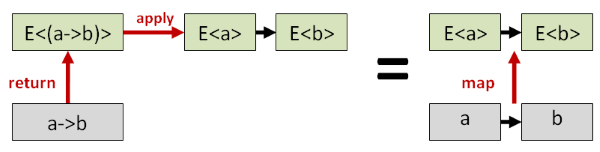
This trick also means that our infix notation can be simplified a little. The initial return then apply can be replaced with map,
and we so typically create an infix operator for map as well, such as <!> in F#.
let resultOption2 =
let (<!>) = Option.map
let (<*>) = Option.apply
add <!> (Some 2) <*> (Some 3)
// resultOption2 = Some 5
let resultList2 =
let (<!>) = List.map
let (<*>) = List.apply
add <!> [1;2] <*> [10;20]
// resultList2 = [11; 21; 12; 22]
This makes the code look more like using the function normally. That is, instead of the normal add x y, we can use the similar looking add <!> x <*> y,
but now x and y can be elevated values rather than normal values. Some people have even called this style "overloaded whitespace"!
Here's one more for fun:
let batman =
let (<!>) = List.map
let (<*>) = List.apply
// string concatenation using +
(+) <!> ["bam"; "kapow"; "zap"] <*> ["!"; "!!"]
// result =
// ["bam!"; "bam!!"; "kapow!"; "kapow!!"; "zap!"; "zap!!"]
The properties of a correct apply/return implementation
As with map, a correct implementation of the apply/return pair should have some properties that are true no matter what elevated world we are working with.
There are four so-called "Applicative Laws",
and an Applicative Functor (in the programming sense) is defined as a generic data type constructor -- E<T> -- plus a pair of
functions (apply and return) that obey the applicative laws.
Just as with the laws for map, these laws are quite sensible. I'll show two of them.
The first law says that if you take the id function in the normal world, and you lift it into the elevated world with return, and then you do apply,
the new function, which is of type E<a> -> E<a>, should be the same as the id function in the elevated world.

The second law says that if you take a function f and a value x in the normal world, and you apply f to x to get a result (y, say), and then lift the result using return,
the resulting value should be the same as if you lifted f and x into the elevated world first, and then applied them there afterwards.
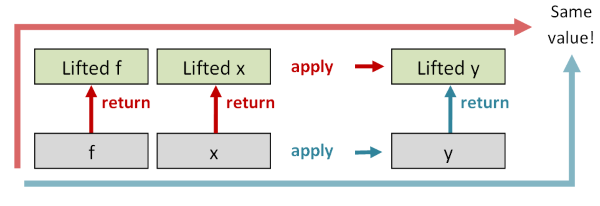
The other two laws are not so easily diagrammed, so I won't document them here, but together the laws ensure that any implementation is sensible.
The liftN family of functions
Common Names: lift2, lift3, lift4 and similar
Common Operators: None
What it does: Combines two (or three, or four) elevated values using a specified function
Signature:
lift2: (a->b->c) -> E<a> -> E<b> -> E<c>,
lift3: (a->b->c->d) -> E<a> -> E<b> -> E<c> -> E<d>,
etc.
Description
The apply and return functions can be used to define a series of helper functions liftN (lift2, lift3, lift4, etc)
that take a normal function with N parameters (where N=2,3,4, etc) and transform it to a corresponding elevated function.
Note that lift1 is just map, and so it is not usually defined as a separate function.
Here's what an implementation might look like:
module Option =
let (<*>) = apply
let (<!>) = Option.map
let lift2 f x y =
f <!> x <*> y
let lift3 f x y z =
f <!> x <*> y <*> z
let lift4 f x y z w =
f <!> x <*> y <*> z <*> w
Here's a visual representation of lift2:
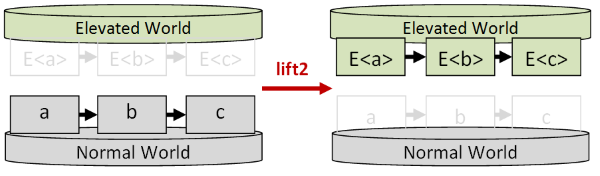
The lift series of functions can be used to make code a bit more readable because,
by using one of the pre-made lift functions, we can avoid the <*> syntax.
First, here's an example of lifting a two-parameter function:
// define a two-parameter function to test with
let addPair x y = x + y
// lift a two-param function
let addPairOpt = Option.lift2 addPair
// call as normal
addPairOpt (Some 1) (Some 2)
// result => Some 3
And here's an example of lifting a three-parameter function:
// define a three-parameter function to test with
let addTriple x y z = x + y + z
// lift a three-param function
let addTripleOpt = Option.lift3 addTriple
// call as normal
addTripleOpt (Some 1) (Some 2) (Some 3)
// result => Some 6
Interpreting "lift2" as a "combiner"
There is an alternative interpretation of apply as a "combiner" of elevated values, rather than as function application.
For example, when using lift2, the first parameter is a parameter specifying how to combine the values.
Here's an example where the same values are combined in two different ways: first with addition, then with multiplication.
Option.lift2 (+) (Some 2) (Some 3) // Some 5
Option.lift2 (*) (Some 2) (Some 3) // Some 6
Going further, can we eliminate the need for this first function parameter and have a generic way of combining the values?
Why, yes we can! We can just use a tuple constructor to combine the values. When we do this we are combining the values without making any decision about how they will be used yet.
Here's what it looks like in a diagram:

and here's how you might implement it for options and lists:
// define a tuple creation function
let tuple x y = x,y
// create a generic combiner of options
// with the tuple constructor baked in
let combineOpt x y = Option.lift2 tuple x y
// create a generic combiner of lists
// with the tuple constructor baked in
let combineList x y = List.lift2 tuple x y
Let's see what happens when we use the combiners:
combineOpt (Some 1) (Some 2)
// Result => Some (1, 2)
combineList [1;2] [100;200]
// Result => [(1, 100); (1, 200); (2, 100); (2, 200)]
Now that we have an elevated tuple, we can work with the pair in any way we want, we just need to use map to do the actual combining.
Want to add the values? Just use + in the map function:
combineOpt (Some 2) (Some 3)
|> Option.map (fun (x,y) -> x + y)
// Result => // Some 5
combineList [1;2] [100;200]
|> List.map (fun (x,y) -> x + y)
// Result => [101; 201; 102; 202]
Want to multiply the values? Just use * in the map function:
combineOpt (Some 2) (Some 3)
|> Option.map (fun (x,y) -> x * y)
// Result => Some 6
combineList [1;2] [100;200]
|> List.map (fun (x,y) -> x * y)
// Result => [100; 200; 200; 400]
And so on. Obviously, real-world uses would be somewhat more interesting.
Defining apply in terms of lift2
Interestingly, the lift2 function above can be actually used as an alternative basis for defining apply.
That is, we can define apply in terms of the lift2 function by setting the combining function to be just function application.
Here's a demonstration of how this works for Option:
module Option =
/// define lift2 from scratch
let lift2 f xOpt yOpt =
match xOpt,yOpt with
| Some x,Some y -> Some (f x y)
| _ -> None
/// define apply in terms of lift2
let apply fOpt xOpt =
lift2 (fun f x -> f x) fOpt xOpt
This alternative approach is worth knowing about because for some types it's easier to define lift2 than apply.
Combining missing or bad data
Notice that in all the combiners we've looked at, if one of the elevated values is "missing" or "bad" somehow, then the overall result is also bad.
For example, with combineList, if one of the parameters is an empty list, the result is also an empty list,
and with combineOpt, if one of the parameters is None, the result is also None.
combineOpt (Some 2) None
|> Option.map (fun (x,y) -> x + y)
// Result => None
combineList [1;2] []
|> List.map (fun (x,y) -> x * y)
// Result => Empty list
It's possible to create an alternative kind of combiner that ignores missing or bad values, just as adding "0" to a number is ignored. For more information, see my post on "Monoids without tears".
One sided combiners <* and *>
In some cases you might have two elevated values, and want to discard the value from one side or the other.
Here's an example for lists:
let ( <* ) x y =
List.lift2 (fun left right -> left) x y
let ( *> ) x y =
List.lift2 (fun left right -> right) x y
We can then combine a 2-element list and a 3-element list to get a 6-element list as expected, but the contents come from only one side or the other.
[1;2] <* [3;4;5] // [1; 1; 1; 2; 2; 2]
[1;2] *> [3;4;5] // [3; 4; 5; 3; 4; 5]
We can turn this into a feature! We can replicate a value N times by crossing it with [1..n].
let repeat n pattern =
[1..n] *> pattern
let replicate n x =
[1..n] *> [x]
repeat 3 ["a";"b"]
// ["a"; "b"; "a"; "b"; "a"; "b"]
replicate 5 "A"
// ["A"; "A"; "A"; "A"; "A"]
Of course, this is by no means an efficient way to replicate a value, but it does show that starting with just the two functions apply and return,
you can build up some quite complex behavior.
On a more practical note though, why might this "throwing away data" be useful? Well in many cases, we might not want the values, but we do want the effects.
For example, in a parser, you might see code like this:
let readQuotedString =
readQuoteChar *> readNonQuoteChars <* readQuoteChar
In this snippet, readQuoteChar means "match and read a quote character from the input stream" and
readNonQuoteChars means "read a series of non-quote characters from the input stream".
When we are parsing a quoted string we want ensure the input stream that contains the quote character is read, but we don't care about the quote characters themselves, just the inner content.
Hence the use of *> to ignore the leading quote and <* to ignore the trailing quote.
The zip function and ZipList world
Common Names: zip, zipWith, map2
Common Operators: <*> (in the context of ZipList world)
What it does: Combines two lists (or other enumerables) using a specified function
Signature: E<(a->b->c)> -> E<a> -> E<b> -> E<c> where E is a list or other enumerable type,
or E<a> -> E<b> -> E<a,b> for the tuple-combined version.
Description
Some data types might have more than one valid implementation of apply. For example, there is another possible implementation of apply for lists,
commonly called ZipList or some variant of that.
In this implementation, the corresponding elements in each list are processed at the same time, and then both lists are shifted to get the next element.
That is, the list of functions [f; g] applied to the list of values [x; y] becomes the two-element list [f x; g y]
// alternate "zip" implementation
// [f;g] apply [x;y] becomes [f x; g y]
let rec zipList fList xList =
match fList,xList with
| [],_
| _,[] ->
// either side empty, then done
[]
| (f::fTail),(x::xTail) ->
// new head + new tail
(f x) :: (zipList fTail xTail)
// has type : ('a -> 'b) -> 'a list -> 'b list
WARNING: This implementation is just for demonstration. It's not tail-recursive, so don't use it for large lists!
If the lists are of different lengths, some implementations throw an exception (as the F# library functions List.map2 and List.zip do),
while others silently ignore the extra data (as the implementation above does).
Ok, let's see it in use:
let add10 x = x + 10
let add20 x = x + 20
let add30 x = x + 30
let result =
let (<*>) = zipList
[add10; add20; add30] <*> [1; 2; 3]
// result => [11; 22; 33]
Note that the result is [11; 22; 33] -- only three elements. If we had used the standard List.apply, there would have been nine elements.
Interpreting "zip" as a "combiner"
We saw above that List.apply, or rather List.lift2, could be intepreted as a combiner. Similarly, so can zipList.
let add x y = x + y
let resultAdd =
let (<*>) = zipList
[add;add] <*> [1;2] <*> [10;20]
// resultAdd = [11; 22]
// [ (add 1 10); (add 2 20) ]
Note that we can't just have one add function in the first list -- we have to have one add for every element in the second and third lists!
That could get annoying, so often, a "tupled" version of zip is used, whereby you don't specify a combining function at all, and just get back a list of tuples instead,
which you can then process later using map.
This is the same approach as was used in the combine functions discussed above, but for zipList.
ZipList world
In standard List world, there is an apply and a return. But with our different version of apply we can create a different version of List world
called ZipList world.
ZipList world is quite different from the standard List world.
In ZipList world, the apply function is implemented as above. But more interestingly, ZipList world has a completely different
implementation of return compared with standard List world.
In the standard List world, return is just a list with a single element, but for
ZipList world, it has to be an infinitely repeated value!
In a non-lazy language like F#, we can't do this, but if we replace List with Seq (aka IEnumerable) then
we can create an infinitely repeated value, as shown below:
module ZipSeq =
// define "return" for ZipSeqWorld
let retn x = Seq.initInfinite (fun _ -> x)
// define "apply" for ZipSeqWorld
// (where we can define apply in terms of "lift2", aka "map2")
let apply fSeq xSeq =
Seq.map2 (fun f x -> f x) fSeq xSeq
// has type : ('a -> 'b) seq -> 'a seq -> 'b seq
// define a sequence that is a combination of two others
let triangularNumbers =
let (<*>) = apply
let addAndDivideByTwo x y = (x + y) / 2
let numbers = Seq.initInfinite id
let squareNumbers = Seq.initInfinite (fun i -> i * i)
(retn addAndDivideByTwo) <*> numbers <*> squareNumbers
// evaulate first 10 elements
// and display result
triangularNumbers |> Seq.take 10 |> List.ofSeq |> printfn "%A"
// Result =>
// [0; 1; 3; 6; 10; 15; 21; 28; 36; 45]
This example demonstrates that an elevated world is not just a data type (like the List type) but consists of the datatype and the functions that work with it. In this particular case, "List world" and "ZipList world" share the same data type but have quite different environments.
What types support map and apply and return?
So far we have defined all these useful functions in an abstract way. But how easy is it to find real types that have implementations of them, including all the various laws?
The answer is: very easy! In fact almost all types support these set of functions. You'd be hard-pressed to find a useful type that didn't.
That means that map and apply and return are available (or can be easily implemented) for standard types such as Option, List, Seq, Async, etc.,
and also any types you are likely to define yourself.
Summary
In this post, I described three core functions for lifting simple "normal" values to elevated worlds: map, return, and apply,
plus some derived functions like liftN and zip.
In practice however, things are not that simple. We frequently have to work with functions that cross between the worlds. Their input is in the normal world but their output is in the elevated world.
In the next post we'll show how these world-crossing functions can be lifted to the elevated world as well.