Dr Frankenfunctor and the Monadster

UPDATE: Slides and video from my talk on this topic

Warning! This post contains gruesome topics, strained analogies, discussion of monads

For generations, we have been captivated by the tragic story of Dr Frankenfunctor. The fascination with vital forces, the early experiments with electricity and galvanism, and finally the breakthough culminating in the bringing to life of a collection of dead body parts -- the Monadster.

But then, as we all know, the creature escaped and the free Monadster rampaged through computer science conferences, bringing fear to the hearts of even the most seasoned programmers.

CAPTION: The terrible events at the 1990 ACM Conference on LISP and Functional Programming.

I will not repeat the details here; the story is still too terrible to recall.

But in all the millions of words devoted to this tragedy, one topic has never been satisfactorily addressed.

How was the creature assembled and brought to life?

We know that Dr Frankenfunctor built the creature from dead body parts, and then animated them in a single instant, using a bolt of lightning to create the vital force.

But the various body parts had to be assembled into a whole, and the vital force had to be transmitted through the assembly in the appropriate manner, and all this done in a split second, in the moment that the lightning struck.

I have devoted many years of research into this matter, and recently, at great expense, I have managed to obtain Dr Frankenfunctor's personal laboratory notebooks.

So at last, I can present Dr Frankenfunctor's technique to the world. Use it as you will. I do not make any judgements as to its morality, after all, it is not for mere developers to question the real-world effects of what we build.

Background

To start with, you need to understand the fundamental process involved.

First, you must know that no whole body was available to Dr Frankenfunctor. Instead, the creature was created from an assemblage of body parts -- arms, legs, brain, heart -- whose provenances were murky and best left unspoken.

Dr Frankenfunctor started with a dead body part, and infused it with some amount of vital force. The result was two things: a now live body part, and the remaining, diminished, vital force, because of course some of the vital force was transferred to the live part.

Here is a diagram demonstrating the principle:

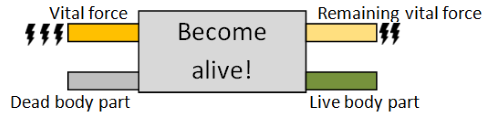
But this creates only one body part. How can we create more than one? This is the challenge that faced Dr Frankenfunctor.

The first problem is that we only have a limited quantity of the vital force. This means that when we need to animate a second body part, we have available only the remaining vital force from a previous step.

How can we connect the two steps together so that the vital force from the first step is fed into the input of the second step?

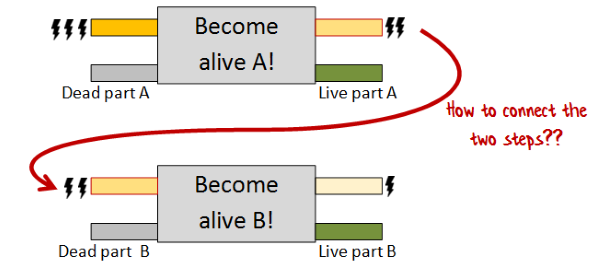
Even if we have chained the steps correctly, we need to take the various live body parts and combine them somehow. But we only have access to live body parts during the moment of creation. How can we combine them in that split second?

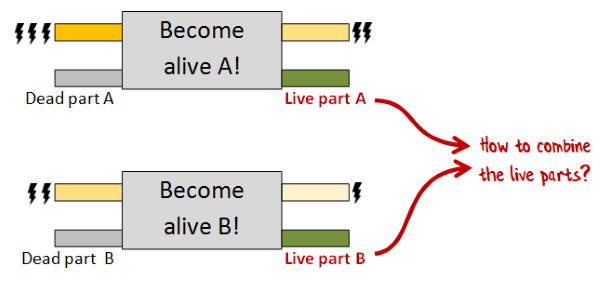
It was Dr Frankenfunctor's genius that led to an elegant approach that solved both of these problems, the approach that I will present to you now.

The common context

Before discussing the particulars of assembling the body parts, we should spend a moment on common functionality that is required for the rest of the procedure.

First, we need a label type. Dr Frankenfunctor was very disciplined in labeling the source of every part used.

type Label = string

The vital force we will model with a simple record type:

type VitalForce = {units:int}

Since we will be using vital force frequently, we will create a function that extracts one unit and returns a tuple of the unit and remaining force.

let getVitalForce vitalForce = 
   let oneUnit = {units = 1}
   let remaining = {units = vitalForce.units-1}  // decrement
   oneUnit, remaining  // return both

The Left Leg

With the common code out of the way, we can return to the substance.

Dr Frankenfunctor's notebooks record that the lower extremities were created first. There was a left leg lying around in the laboratory, and that was the starting point.

type DeadLeftLeg = DeadLeftLeg of Label

From this leg, a live leg could be created with the same label and one unit of vital force.

type LiveLeftLeg = LiveLeftLeg of Label * VitalForce

The type signature for the creation function would thus look like this:

type MakeLiveLeftLeg = 
    DeadLeftLeg * VitalForce -> LiveLeftLeg * VitalForce

And the actual implementation like this:

let makeLiveLeftLeg (deadLeftLeg,vitalForce) = 
    // get the label from the dead leg using pattern matching
    let (DeadLeftLeg label) = deadLeftLeg
    // get one unit of vital force
    let oneUnit, remainingVitalForce = getVitalForce vitalForce 
    // create a live leg from the label and vital force
    let liveLeftLeg = LiveLeftLeg (label,oneUnit)
    // return the leg and the remaining vital force
    liveLeftLeg, remainingVitalForce

As you can see, this implementation matched the earlier diagram precisely.

At this point Dr Frankenfunctor had two important insights.

The first insight was that, thanks to currying, the function could be converted from a function taking a tuple to a two parameter function, with each parameter passed in turn.

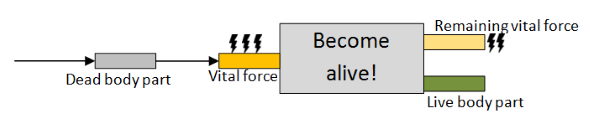
And the code now looked like this:

type MakeLiveLeftLeg = 
    DeadLeftLeg -> VitalForce -> LiveLeftLeg * VitalForce 

let makeLiveLeftLeg deadLeftLeg vitalForce = 
    let (DeadLeftLeg label) = deadLeftLeg
    let oneUnit, remainingVitalForce = getVitalForce vitalForce 
    let liveLeftLeg = LiveLeftLeg (label,oneUnit)
    liveLeftLeg, remainingVitalForce

The second insight was that this same code can be interpreted as a function that in turn returns a "becomeAlive" function.

That is, we have the dead part on hand, but we won't have any vital force until the final moment, so why not process the dead part right now and return a function that can be used when the vital force becomes available.

In other words, we pass in a dead part, and we get back a function that creates a live part when given some vital force.

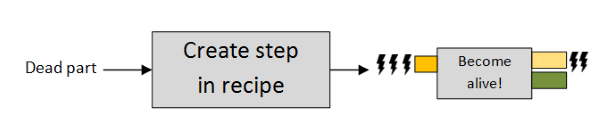
These "become alive" functions can then be treated as "steps in a recipe", assuming we can find some way of combining them.

The code looks like this now:

type MakeLiveLeftLeg = 
    DeadLeftLeg -> (VitalForce -> LiveLeftLeg * VitalForce)

let makeLiveLeftLeg deadLeftLeg = 
    // create an inner intermediate function
    let becomeAlive vitalForce = 
        let (DeadLeftLeg label) = deadLeftLeg
        let oneUnit, remainingVitalForce = getVitalForce vitalForce 
        let liveLeftLeg = LiveLeftLeg (label,oneUnit)
        liveLeftLeg, remainingVitalForce    
    // return it
    becomeAlive

It may not be obvious, but this is exactly the same code as the previous version, just written slightly differently.

This curried function (with two parameters) can be interpreted as a normal two parameter function, or it can be interpreted as a one parameter function that returns another one parameter function.

If this is not clear, consider the much simpler example of a two parameter add function:

let add x y = 
    x + y

Because F# curries functions by default, that implementation is exactly the same as this one:

let add x = 
    fun y -> x + y

Which, if we define an intermediate function, is also exactly the same as this one:

let add x = 
    let addX y = x + y
    addX // return the function

Creating the Monadster type

Looking ahead, we can see that we can use a similar approach for all the functions that create live body parts.

All those functions will return a function that has a signature like: VitalForce -> LiveBodyPart * VitalForce.

To make our life easy, let's give that function signature a name, M, which stands for "Monadster part generator", and give it a generic type parameter 'LiveBodyPart so that we can use it with many different body parts.

type M<'LiveBodyPart> = 
    VitalForce -> 'LiveBodyPart * VitalForce

We can now explicitly annotate the return type of the makeLiveLeftLeg function with :M<LiveLeftLeg>.

let makeLiveLeftLeg deadLeftLeg :M<LiveLeftLeg> = 
    let becomeAlive vitalForce = 
        let (DeadLeftLeg label) = deadLeftLeg
        let oneUnit, remainingVitalForce = getVitalForce vitalForce 
        let liveLeftLeg = LiveLeftLeg (label,oneUnit)
        liveLeftLeg, remainingVitalForce    
    becomeAlive

The rest of the function is unchanged because the becomeAlive return value is already compatible with M<LiveLeftLeg>.

But I don't like having to explicitly annotate all the time. How about we wrap the function in a single case union -- call it "M" -- to give it its own distinct type? Like this:

type M<'LiveBodyPart> = 
    M of (VitalForce -> 'LiveBodyPart * VitalForce)

That way, we can distinguish between a "Monadster part generator" and an ordinary function returning a tuple.

To use this new definition, we need to tweak the code to wrap the intermediate function in the single case union M when we return it, like this:

let makeLiveLeftLegM deadLeftLeg  = 
    let becomeAlive vitalForce = 
        let (DeadLeftLeg label) = deadLeftLeg
        let oneUnit, remainingVitalForce = getVitalForce vitalForce 
        let liveLeftLeg = LiveLeftLeg (label,oneUnit)
        liveLeftLeg, remainingVitalForce    
    // changed!        
    M becomeAlive // wrap the function in a single case union

For this last version, the type signature will be correctly inferred without having to specify it explicitly: a function that takes a dead left leg and returns an "M" of a live leg:

val makeLiveLeftLegM : DeadLeftLeg -> M<LiveLeftLeg>

Note that I've renamed the function makeLiveLeftLegM to make it clear that it returns a M of LiveLeftLeg.

The meaning of M

So what does this "M" type mean exactly? How can we make sense of it?

One helpful way is to think of a M<T> as a recipe for creating a T. You give me some vital force and I'll give you back a T.

But how can an M<T> create a T out of nothing?

That's where functions like makeLiveLeftLegM are critically important. They take a parameter and "bake" it into the result. As a result, you will see lots of "M-making" functions with similar signatures, all looking something like this:

Or in code terms:

DeadPart -> M<LivePart>

The challenge now will be how to combine these in an elegant way.

Testing the left leg

Ok, let's test what we've got so far.

We'll start by creating a dead leg and use makeLiveLeftLegM on it to get an M<LiveLeftLeg>.

let deadLeftLeg = DeadLeftLeg "Boris"
let leftLegM = makeLiveLeftLegM deadLeftLeg

What is leftLegM? It's a recipe for creating a live left leg, given some vital force.

What's useful is that we can create this recipe up front, before the lightning strikes.

Now let's pretend that the storm has arrived, the lightning has struck, and 10 units of vital force are now available:

let vf = {units = 10}

Now, inside the leftLegM is a function which we can apply to the vital force. But first we need to get the function out of the wrapper using pattern matching.

let (M innerFn) = leftLegM

And then we can run the inner function to get the live left leg and the remaining vital force:

let liveLeftLeg, remainingAfterLeftLeg = innerFn vf

The results look like this:

val liveLeftLeg : LiveLeftLeg = 
   LiveLeftLeg ("Boris",{units = 1;})
val remainingAfterLeftLeg : VitalForce = 
   {units = 9;}

You can see that a LiveLeftLeg was created successfully and that the remaining vital force is reduced to 9 units now.

This pattern matching is awkward, so let's create a helper function that both unwraps the inner function and calls it, all in one go.

We'll call it runM and it looks like this:

let runM (M f) vitalForce = f vitalForce

So the test code above would now be simplified to this:

let liveLeftLeg, remainingAfterLeftLeg = runM leftLegM vf

So now, finally, we have a function that can create a live left leg.

It took a while to get it working, but we've also built some useful tools and concepts that we can use moving forwards.

The Right Leg

Now that we know what we are doing, we should be able to use the same techniques for the other body parts now.

How about a right leg then?

Unfortunately, according to the notebook, Dr Frankenfunctor could not find a right leg in the laboratory. The problem was solved with a hack... but we'll come to that later.

The Left Arm

Next, the arms were created, starting with the left arm.

But there was a problem. The laboratory only had a broken left arm lying around. The arm had to be healed before it could be used in the final body.

Now Dr Frankenfunctor, being a doctor, did know how to heal a broken arm, but only a live one. Trying to heal a dead broken arm would be impossible.

In code terms, we have this:

type DeadLeftBrokenArm = DeadLeftBrokenArm of Label 

// A live version of the broken arm.
type LiveLeftBrokenArm = LiveLeftBrokenArm of Label * VitalForce

// A live version of a heathly arm, with no dead version available
type LiveLeftArm = LiveLeftArm of Label * VitalForce

// An operation that can turn a broken left arm into a heathly left arm
type HealBrokenArm = LiveLeftBrokenArm -> LiveLeftArm

The challenge was therefore this: how can we make a live left arm out the material we have on hand?

First, we have to rule out creating a LiveLeftArm from a DeadLeftUnbrokenArm, as there isn't any such thing. Nor can we convert a DeadLeftBrokenArm into a healthy LiveLeftArm directly.

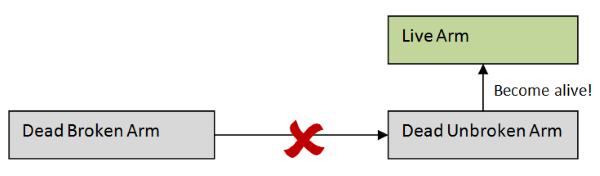
But what we can do is turn the DeadLeftBrokenArm into a live broken arm and then heal the live broken arm, yes?

No, I'm afraid that won't work. We can't create live parts directly, we can only create live parts in the context of the M recipe.

What we need to do then is create a special version of healBrokenArm (call it healBrokenArmM) that converts a M<LiveBrokenArm> to a M<LiveArm>.

But how do we create such a function? And how can we reuse healBrokenArm as part of it?

Let's start with the most straightforward implementation.

First, since the function will return an M something, it will have the same form as the makeLiveLeftLegM function that we saw earlier. We'll need to create an inner function that has a vitalForce parameter, and then return it wrapped in an M.

But unlike the function that we saw earlier, this one has an M as parameter too (an M<LiveBrokenArm>). How can we extract the data we need from this input?

Simple, just run it with some vitalForce. And where are we going to get the vitalForce from? From the parameter to the inner function!

So our finished version will look like this:

// implementation of HealBrokenArm
let healBrokenArm (LiveLeftBrokenArm (label,vf)) = LiveLeftArm (label,vf)

/// convert a M<LiveLeftBrokenArm> into a M<LiveLeftArm>
let makeHealedLeftArm brokenArmM = 

    // create a new inner function that takes a vitalForce parameter
    let healWhileAlive vitalForce = 
        // run the incoming brokenArmM with the vitalForce 
        // to get a broken arm
        let brokenArm,remainingVitalForce = runM brokenArmM vitalForce 

        // heal the broken arm
        let healedArm = healBrokenArm brokenArm

        // return the healed arm and the remaining VitalForce
        healedArm, remainingVitalForce

    // wrap the inner function and return it
    M healWhileAlive

If we evaluate this code, we get the signature:

val makeHealedLeftArm : M<LiveLeftBrokenArm> -> M<LiveLeftArm>

which is exactly what we want!

But not so fast -- we can do better.

We've hard-coded the healBrokenArm transformation in there. What happens if we want to do some other transformation, and for some other body part? Can we make this function a bit more generic?

Yes, it's easy. All we need to is pass in a function ("f" say) that transforms the body part, like this:

let makeGenericTransform f brokenArmM = 

    // create a new inner function that takes a vitalForce parameter
    let healWhileAlive vitalForce = 
        let brokenArm,remainingVitalForce = runM brokenArmM vitalForce 

        // heal the broken arm using passed in f
        let healedArm = f brokenArm
        healedArm, remainingVitalForce

    M healWhileAlive

What's amazing about this is that by parameterizing that one transformation with the f parameter, the whole function becomes generic!

We haven't made any other changes, but the signature for makeGenericTransform no longer refers to arms. It works with anything!

val makeGenericTransform : f:('a -> 'b) -> M<'a> -> M<'b>

Introducing mapM

Since it is so generic now, the names are confusing. Let's rename it. I'll call it mapM. It works with any body part and any transformation.

Here's the implementation, with the internal names fixed up too.

let mapM f bodyPartM = 
    let transformWhileAlive vitalForce = 
        let bodyPart,remainingVitalForce = runM bodyPartM vitalForce 
        let updatedBodyPart = f bodyPart
        updatedBodyPart, remainingVitalForce
    M transformWhileAlive

In particular, it works with the healBrokenArm function, so to create a version of "heal" that has been lifted to work with Ms we can just write this:

let healBrokenArmM = mapM healBrokenArm

The importance of mapM

One way of thinking about mapM is that it is a "function converter". Given any "normal" function, it converts it to a function where the input and output are Ms.

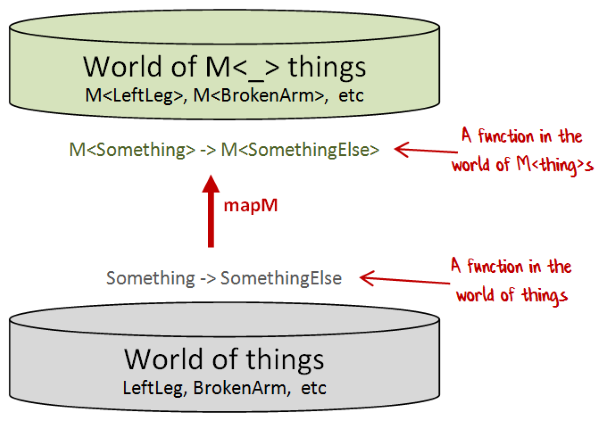
Functions similar to mapM crop up in many situations. For example, Option.map transforms a "normal" function into a function whose inputs and outputs are options. Similarly, List.map transforms a "normal" function into a function whose inputs and outputs are lists. And there are many other examples.

// map works with options
let healBrokenArmO = Option.map healBrokenArm
// LiveLeftBrokenArm option -> LiveLeftArm option

// map works with lists
let healBrokenArmL = List.map healBrokenArm
// LiveLeftBrokenArm list -> LiveLeftArm list

What might be new to you is that the "wrapper" type M contains a function, not a simple data structure like Option or List. That might make your head hurt!

In addition, the diagram above implies that M could wrap any normal type and mapM could map any normal function.

Let's try it and see!

let isEven x = (x%2 = 0)   // int -> bool
// map it
let isEvenM = mapM isEven  // M<int> -> M<bool>

let isEmpty x = (String.length x)=0  // string -> bool
// map it
let isEmptyM = mapM isEmpty          // M<string> -> M<bool>

So, yes, it works!

Testing the left arm

Again, let's test what we've got so far.

We'll start by creating a dead broken arm and use makeLiveLeftBrokenArm on it to get an M<BrokenLeftArm>.

let makeLiveLeftBrokenArm deadLeftBrokenArm = 
    let (DeadLeftBrokenArm label) = deadLeftBrokenArm
    let becomeAlive vitalForce = 
        let oneUnit, remainingVitalForce = getVitalForce vitalForce 
        let liveLeftBrokenArm = LiveLeftBrokenArm (label,oneUnit)
        liveLeftBrokenArm, remainingVitalForce    
    M becomeAlive

/// create a dead Left Broken Arm
let deadLeftBrokenArm = DeadLeftBrokenArm "Victor"

/// create a M<BrokenLeftArm> from the dead one
let leftBrokenArmM = makeLiveLeftBrokenArm deadLeftBrokenArm

Now we can use mapM and healBrokenArm to convert the M<BrokenLeftArm> into a M<LeftArm>:

let leftArmM = leftBrokenArmM |> mapM healBrokenArm

What we have now in leftArmM is a recipe for creating a unbroken and live left arm. All we need to do is add some vital force.

As before, we can do all these things up front, before the lightning strikes.

Now when the storm arrives, and the lightning has struck, and vital force is available, we can run leftArmM with the vital force...

let vf = {units = 10}

let liveLeftArm, remainingAfterLeftArm = runM leftArmM vf

...and we get this result:

val liveLeftArm : LiveLeftArm = 
    LiveLeftArm ("Victor",{units = 1;})
val remainingAfterLeftArm : 
    VitalForce = {units = 9;}

A live left arm, just as we wanted.

The Right Arm

On to the right arm next.

Again, there was a problem. Dr Frankenfunctor's notebooks record that there was no whole arm available. However there was a lower arm and an upper arm...

type DeadRightLowerArm = DeadRightLowerArm of Label 
type DeadRightUpperArm = DeadRightUpperArm of Label

...which could be turned into corresponding live ones:

type LiveRightLowerArm = LiveRightLowerArm of Label * VitalForce
type LiveRightUpperArm = LiveRightUpperArm of Label * VitalForce

Dr Frankenfunctor decided to do surgery to join the two arm sections into a whole arm.

// define the whole arm
type LiveRightArm = {
    lowerArm : LiveRightLowerArm
    upperArm : LiveRightUpperArm
    }

// surgery to combine the two arm parts
let armSurgery lowerArm upperArm =
    {lowerArm=lowerArm; upperArm=upperArm}

As with the broken arm, the surgery could only be done with live parts. Doing that with dead parts would be yucky and gross.

But also, as with the broken arm, we don't have access to the live parts directly, only within the context of an M wrapper.

In other words we need to convert our armSurgery function that works with normal live parts, and convert it into a armSurgeryM function that works with Ms.

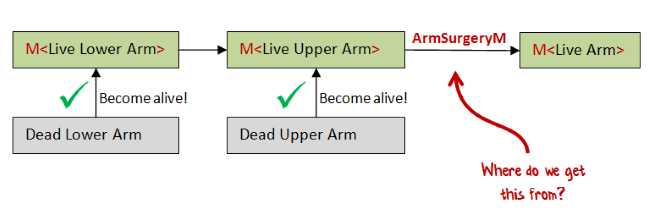
We can use the same approach as we did before:

• create a inner function that takes a vitalForce parameter
• run the incoming parameters with the vitalForce to extract the data
• from the inner function return the new data after surgery
• wrap the inner function in an "M" and return it

Here's the code:

/// convert a M<LiveRightLowerArm> and  M<LiveRightUpperArm> into a M<LiveRightArm>
let makeArmSurgeryM_v1 lowerArmM upperArmM =

    // create a new inner function that takes a vitalForce parameter
    let becomeAlive vitalForce = 
        // run the incoming lowerArmM with the vitalForce 
        // to get the lower arm
        let liveLowerArm,remainingVitalForce = runM lowerArmM vitalForce 

        // run the incoming upperArmM with the remainingVitalForce 
        // to get the upper arm
        let liveUpperArm,remainingVitalForce2 = runM upperArmM remainingVitalForce 

        // do the surgery to create a liveRightArm
        let liveRightArm = armSurgery liveLowerArm liveUpperArm

        // return the whole arm and the SECOND remaining VitalForce
        liveRightArm, remainingVitalForce2  

    // wrap the inner function and return it
    M becomeAlive

One big difference from the broken arm example is that we have two parameters, of course. When we run the second parameter (to get the liveUpperArm), we must be sure to pass in the remaining vital force after the first step, not the original one.

And then, when we return from the inner function, we must be sure to return remainingVitalForce2 (the remainder after the second step) not any other one.

If we compile this code, we get:

M<LiveRightLowerArm> -> M<LiveRightUpperArm> -> M<LiveRightArm>

which is just the signature we are looking for.

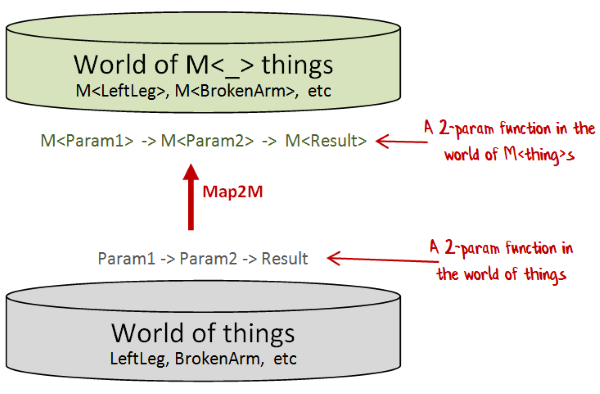
Introducing map2M

But as before, why not make this more generic? We don't need to hard-code armSurgery -- we can pass it as a parameter.

We'll call the more generic function map2M -- just like mapM but with two parameters.

Here's the implementation:

let map2M f m1 m2 =
    let becomeAlive vitalForce = 
        let v1,remainingVitalForce = runM m1 vitalForce 
        let v2,remainingVitalForce2 = runM m2 remainingVitalForce  
        let v3 = f v1 v2
        v3, remainingVitalForce2    
    M becomeAlive

And it has the signature:

f:('a -> 'b -> 'c) -> M<'a> -> M<'b> -> M<'c>

Just as with mapM we can interpret this function as a "function converter" that converts a "normal" two parameter function into a function in the world of M.

Testing the right arm

Again, let's test what we've got so far.

As always, we need some functions to convert the dead parts into live parts.

let makeLiveRightLowerArm (DeadRightLowerArm label) = 
    let becomeAlive vitalForce = 
        let oneUnit, remainingVitalForce = getVitalForce vitalForce 
        let liveRightLowerArm = LiveRightLowerArm (label,oneUnit)
        liveRightLowerArm, remainingVitalForce    
    M becomeAlive

let makeLiveRightUpperArm (DeadRightUpperArm label) = 
    let becomeAlive vitalForce = 
        let oneUnit, remainingVitalForce = getVitalForce vitalForce 
        let liveRightUpperArm = LiveRightUpperArm (label,oneUnit)
        liveRightUpperArm, remainingVitalForce    
    M becomeAlive

By the way, are you noticing that there is a lot of duplication in these functions? Me too! We will attempt to fix that later.

Next, we'll create the parts:

let deadRightLowerArm = DeadRightLowerArm "Tom"
let lowerRightArmM = makeLiveRightLowerArm deadRightLowerArm 

let deadRightUpperArm = DeadRightUpperArm "Jerry"
let upperRightArmM = makeLiveRightUpperArm deadRightUpperArm

And then create the function to make a whole arm:

let armSurgeryM  = map2M armSurgery 
let rightArmM = armSurgeryM lowerRightArmM upperRightArmM

As always, we can do all these things up front, before the lightning strikes, building a recipe (or computation if you like) that will do everything we need when the time comes.

When the vital force is available, we can run rightArmM with the vital force...

let vf = {units = 10}

let liveRightArm, remainingFromRightArm = runM rightArmM vf

...and we get this result:

val liveRightArm : LiveRightArm =
    {lowerArm = LiveRightLowerArm ("Tom",{units = 1;});
     upperArm = LiveRightUpperArm ("Jerry",{units = 1;});}

val remainingFromRightArm : VitalForce = 
    {units = 8;}

A live right arm, composed of two subcomponents, just as required.

Also note that the remaining vital force has gone down to eight. We have correctly used up two units of vital force.

Summary

In this post, we saw how to create a M type that wrapped a "become alive" function that in turn could only be activated when lightning struck.

We also saw how various M-values could be processed and combined using mapM (for the broken arm) and map2M (for the arm in two parts).

The code samples used in this post are available on GitHub.

Next time

This exciting tale has more shocks in store for you! Stay tuned for the next installment, when I reveal how the head and body were created.